This article is comparing the results of using a deep learning algorithm, LSTMs, for a regression problem versus simple Neural Networks and ensemble algorithms like Random Forest and XGBoost. The objective is to show that it is important to choose the right algorithm for the problem you are solving.
LSTM (Long Short-term Memory) networks are a type of RNN (Recurrent Neural Networks) networks, one of the many types of Deep Learning algorithms, that are gaining wide use in a variety of problems like Natural Language Processing and image recognition, showing very good results. They are also being mentioned a lot in stock price prediction research and articles.
However, that should be considered with caution. When it comes to forecasting stock prices or other financial data prediction, which is generally time series based, the results are not always accurate and the algorithms take a long time to run. In fact, LSTMs perform worse than simple neural networks or ensemble methods like Random Forest and XGBoost on a lot of financial data prediction problems. Just because an algorithm works well for one set of problems, does not mean it will work well for all problems. This can only be found by trial and error across a variety of problems and algorithms. This doesn’t mean the LSTM algorithm is not good, it’s just that it is not the right one for these problem types.
The example being used for this article is an old Kaggle competition problem – Allstate Insurance Claims Severity. Objective was to predict the cost (severity) of insurance claims using a large data set of factors (over 130 factors and 180,000 rows of data). The data can be downloaded from here – https://www.kaggle.com/c/allstate-claims-severity/overview.
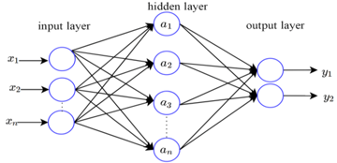
RNNs (Recurrent Neural Networks) are an enhancement to Artificial Neural Networks (ANN). ANNs are basic feed forward neural networks with input/hidden/output layer neurons connected by weighted branches and trained/updated via an optimal gradient descent cost function (activation function like ReLu, sigmoid, etc) which minimises the prediction errors and backpropagates them for updating the weights in the next epoch.
However, ANNs suffer from one limitation, they don’t store or use historic learning like the human brain. They do all their learning/calculations from scratch for each iteration (epoch) of the network, after updating the weights, which incorporate the learning of each iteration of the network. A single hidden layer ANN figure is given below. There can be a large number of neurons and hidden layers with different activation functions which can be tried as part of hyperparameter tuning of the ANN. I won’t go into the details here, there are many books/articles/blogs/videos available online to learn more about ANNs and RNNs.
A good paper on ANNs is – http://www.cs.toronto.edu/~hinton/absps/sciam92.pdf, by Hinton.
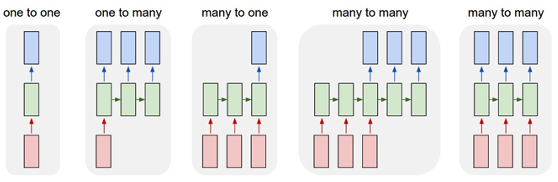
RNNs overcome this limitation by creating a loop within the hidden layers, which feeds the output of the neurons as input to itself and other neurons, a chain of repeating neurons, along with the raw input data. This way the neurons are able to pass their learnings to other neurons in the hidden layers using an activation function like tanh, etc. There are various variations to this model, forward and backward, but effectively they ensure that historic learning is being used and passed in each iteration (epoch). Some possible RNNs figures are given below, from a popular article on RNNs – https://karpathy.github.io/2015/05/21/rnn-effectiveness/, by Andrej Karpathy. It gives a simple and non-technical explanation of the algorithm and its uses.
Two original papers on RNNs by Rumelhart, Hinton, Williams are
- http://www.cs.toronto.edu/~hinton/absps/pdp8.pdf
- https://www.iro.umontreal.ca/~vincentp/ift3395/lectures/backprop_old.pdf
However, RNNs themselves suffer from a limitation, the vanishing gradient problem, As the errors in RNNs are backpropagated all the way back in time to update the weights for each neuron in each epoch, and as they are multiplied their effect becomes even smaller as a result (gradient decay due to derivatives), eventually becoming too small to be relevant. So, the importance of historic information decays with time. This is sub-optimal if you are trying to learn variations in the pattern from historic data, there is a possibility the recent past has less useful information compared to more historic data.
LSTM (Long Short-term Memory) networks partially solve the vanishing gradient problem by learning from historic data (long term dependencies). They do this by replacing the repeating single neuron network layer with a network of combination of 4 neurons (memory cell pipeline) in a specific way. It uses a combination of gates (activation functions like sigmoid, tanh, etc) on the input from previous neurons layers and raw input data (all vectors) to determine what information to forget and remember as part of the output from the memory cell to the pipeline and the next memory cell. Its slightly complex but a simple popular article on RNNs by Christopher Olah is – https://colah.github.io/posts/2015-08-Understanding-LSTMs/. It gives a non-technical explanation of the algorithm and its uses. The figures below are from the blog.
Simple RNN network with self-repeating neuron layer
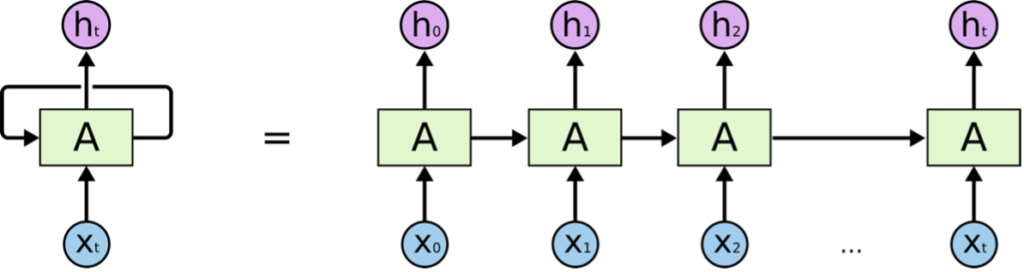
A simple LSTM network with memory cell pipeline, gates and inputs/outputs
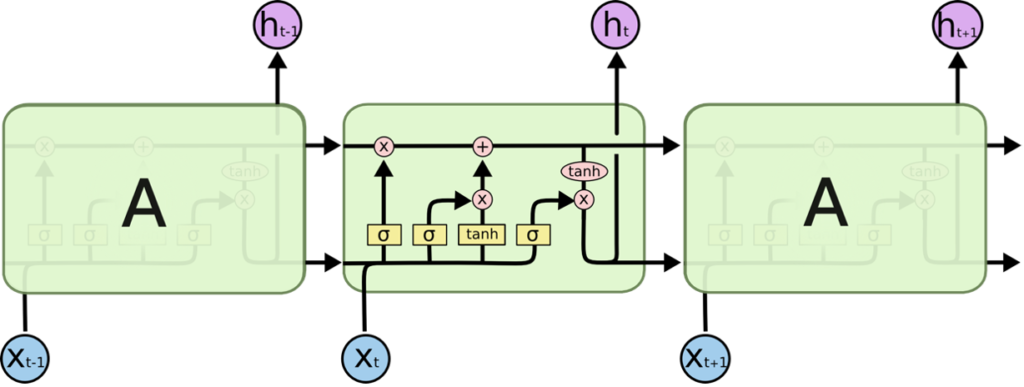
The equations for each gate and memory cell pipeline are explained in the blog. It’s a combination of different activation functions, weights and input vectors to determine the output vectors and performs that across the entire LSTM neural network layer. Algorithms can then use multiple LSTM layers with many memory cell units and different activation functions.
The original LSTM paper by Sepp Hochreiter and Jurgen Schmidhuber is – https://www.researchgate.net/publication/13853244_Long_Short-term_Memory.
The algorithm and math are complex and not straightforward to understand. Better to start with the blog article and then read the paper. It was written in 1997, 25 years ago. So quite amazing to see it being widely used now, most likely due to the availability of cheap and powerful compute and storage. This is similar for a lot of other deep learning algorithms where the research articles were written 20-30 years (Hinton, etc) ago but are only now being widely used and showing very good results.
LSTMs however have their own limitations – long time to train, overfitting, and sensitive to random weight initialization (hence the large training time). This means it requires a lot of compute and data variations. So it’s important to determine whether it’s worth the effort.
Kaggle competition problem – Allstate Insurance Claims Severity. Objective is to predict the cost (severity) of insurance claims using a large data set of factors (over 130 factors and 180,000 rows of data). This is a regression problem requiring values to be predicted on a continuous scale. The data can be downloaded from here – https://www.kaggle.com/c/allstate-claims-severity/overview.
Sample code for comparing different regression algorithms for this problem is given in github –
https://github.com/datawisdomx/LSTMVsOtherRegression–Kaggle–AllStateInsuranceClaims
The code follows the standard data science steps (load, wrangle, encode, scale, train/test split, train, predict, metrics). It compares 4 different regression algorithms on accuracy and time taken to run without hyperparameter tuning, except for LSTM.
- LSTM network
- ANN
- XGBoost
- Random Forest
The results show that
- LSTMs gave the worst results (high Mean Absolute Error MAE) and also take a long time to run, over 2 hrs
- XGBoost and a simple 4 layer ANN gave better results (low MAE) without any hyperparameter tuning. They only took 3-10 minutes to run
- Random Forest takes over 1 hr and gives results similar to XGBoost
- Note – running time is on a basic MacBook Pro, will be faster on better CPU/GPU cloud
Submitting and comparing the results on Kaggle against global leaderboard, the overall results are not good
- No 1 rank score (MAE) is 1109.7
- XGBoost score (MAE) of 1184.5 has rank 2088
The results can be improved by adding more layers to LSTM or ANN networks or hyperparameter tuning for other algorithms, but relatively LSTM will still underperform. That was the objective of this article.
Hope it helps in further understanding of deep learning algorithms and their applications.